Math

Multisets

A multiset in mathematics is a collection of elements where elements can appear multiple times. We will use the word dataset interchangeably to refer to a multiset of test scores.

We will use $X$ to represent a multiset of numbers, and $N$ to represent the size of the multiset. $x_i$ will refer to the $i$th element in the multiset. We will also assume the multiset is ordered from least to greatest. If two or more elements are the same value, they will have different indices, all less than the indices of elements greater than then, and all greater than indices less than them.

Example: $X=\{ 20 , \ $$ 44 , \ $$ 52 , \ $$ 76\}, \ N=4$. Because the multiset is ordered, $x_1 = 20$ is the lowest element of the multiset and $x_N = 76$ is the highest element of the multiset. These two values are referred to as extrema (singular form extremum).

Traditional Curving

Traditional curving, the easiest and most commonly employed form of curving works by scaling up each student's score so that the highest scorer receives a 100. This method can be much improved upon.

Letting $x_i'$ denote a student's new score, their new score can be calculated via $$x_i' = \frac{100}{x_N} x_i$$

Example: If $X=\{ 20, \ $$ 44, \ $$ 52 , \ $$ 76\}, \ X_N = 76$. Then curving this traditionally will result in multiplying each value by $\frac{100}{76}$ yielding roughly $\{26.31, \ $$ 57.89, \ $$ 68.42, \ $$ 100\}$.

Mean

The mean represents the average value of a dataset.

It is denoted by $\mu$ and given by the function $$\mu = \frac{1}{ N }\sum_{i=1}^N x_i$$

Example: Given the dataset $ X=\{20 , \ $$ 44 , \ $$ 52 , \ $$ 76\}, \ N=4$, then $ \frac{1}{ N }\sum_{i=1}^N x_i = \frac{20 \ + \ 44 \ +\ 52\ +\ 76}{4} = 48$, the mean.

Deviation

The deviation of a dataset is a measure of how spread apart the elements are.

It is denoted by $\sigma$ and given by the function $$\sigma = \sqrt{\frac{1}{N}\sum_{i=1}^N (x_i-\mu)^2}$$ The term $(x_i - \mu)^2$ squares the difference between the mean and an element, making sure the value is always positive and making elements further from the average (outliers) more important. These values are then averaged and finally, square-rooted.

Example: For the dataset $X=\{80 , \ $$ 86 , \ $$ 88 , \ $$ 94\}, \ \mu=87$ and $\sigma = 5$ because the elements are all close to the mean. For the dataset $X=\{20 , \ $$ 44 , \ $$ 52 , \ $$ 76\}, \ \mu=48$ and $\sigma = 20$ because the elements are generally far from the mean.

Z-scores

While the deviation measures how spread out a dataset is, a Z-score describes an element's distance from the mean interms of the deviation. A dog that weighs 100 lbs above average is much more rare than an elephant that weighs 100 lbs above average; we can use Z-scores to show this. Z-scores also allow us to compare elements of different distributions, and act as a middleman for adjusting distributions.

The z-score of a particular element is denoted $Z_i$ and given by the formula $$Z_i = \frac{x_i - \mu}{\sigma}$$

Example: The Z-scores of the dataset $X = \{80 , \ $$ 86 , \ $$ 88 , \ $$ 94 \}$ are $\{ -1.4 , \ $$ -0.2 , \ $$ 0.2 , \ $$ 1.4\}$ respectively. The Z-scores of the dataset $X = \{20 , \ $$ 44 , \ $$ 52 , \ $$ 76 \}$ are equal to $\{ -1.4 , \ $$ -0.2 , \ $$ 0.2 , \ $$ 1.4\}$ aswell. Although the datasets have very different distributions, their Z-scores are the same!

Mean and Deviation Curve

When the intended new mean $\mu'$ and intended new deviation $\sigma'$ are supplied by the user, we can proceed directly with the curve function

There is no math nor example to demonstrate this. However, it will become apparent when we employ the curve function.

Curve function

We apply a mathemetical function to each elements z-score to find its newly assigned score.

For each element, we can apply the transformation $$x'_i \ = \ \sigma' Z_i +\mu' \ = \ \sigma' \frac{x_i - \mu}{\sigma} + \mu'$$
Where $x'_i$ is the new score assigned to $x_i$ and $\mu'$ and $\sigma'$ are the new intended mean and deviation respectively.

Example, using $\mu' = 80$ and $\sigma' = 8$, and applying the curve function to the dataset $X = \{20 , \ $$ 44 , \ $$ 52 , \ $$ 76 \}$ the new respective scores are $\{68.8 , \ $$ 78.4 , \ $$ 81.6 , \ $$ 91.2\}$. Comparing this to the results of the tradiational curve, the difference is apparent.

Range Curve

When we constrain a curve to an intended new range, we can either curve the highest and lowest original scores to their respective edges of the new range, or we can place the initial average score at the center of the new range and the score furthest from the average (in either direction) on its respective edge of the new range. Because our curving is type of function known as an affine function, we (in most cases) can only fix our curve function at two values, and cannot use both methods simultaneously. Notably, both methods work concurrently if we normalize the scores (see further discussion below), but this does not necessarily mean normalizing is the best option.

Let $\alpha$ denote the new intended minimum score and $\omega$ denote the new intended maximum score.

To fit the extrema of a dataset to the edges of the new range we define the new intended deviation as $$\sigma' = \frac{ \omega - \alpha}{x_N - x_1}$$ Remember that the dataset $X$is ordered so $x_N - x_1$ is the range of $X$. Next we dataset the new intended mean to $$\mu' = \alpha - \sigma'Z_1$$ This will make it so that when we apply the curve function $f(x)$, $f(x_1)=\alpha$, and $f(x_N) = \omega$. Note $Z_1 \leq 0$.

Example: Setting our new intended range as $\alpha = 60 $ and $ \omega = 100 $, and curving the set $ X= \{20 , \ $$ 44 , \ $$ 52 , \ $$ 76 \} $, we arrive at roughly $ \{60 , \ $$ 77.14 , \ $$ 82.86 , \ $$ 100 \} $.
To fit the mean of the dataset to the center of the new range and the further of the extremum to its respective edge of the range, we let the mean be $$\mu' = \frac{\alpha +\omega}{2}$$ Then we set the deviation so that it scales the furthest element to the edge of the range. $$\sigma' = \frac{\omega-\alpha}{2\max(|Z_1|,|Z_N|) }$$ This will make it so that when we apply the curve function $f(x)$, $f(\mu)=\frac{\alpha + \omega}{2}$. If $|Z_1| > |Z_N|$ then $f(x_1) = \alpha$. If $|Z_1| < |Z_N|$ then $f(x_N) = \omega$.

Example: Setting our new intended range as $ \alpha = 60$ and $ \omega = 100$, and curving the dataset $X=\{50 , \ $$ 68 , \ $$ 79 , \ $$ 98 , \ $$ 100\}, \ \mu=79$ we arrive at roughly $\{60 , \ $$ 72.41 , \ $$ 80 , \ $$ 93.1 , \ $$ 94.48\}$. Because $79$ is the mean of the dataset, it curves to $80$, the center of the range. Because $50$ is further from $79$ than $100$, $50$ curves to $60$, the edge of the new range. $100$, the closer extremum of the dataset, is not curved to $100$, the maximum of the range. A dataset different from the previous datasets was used here to highlight the functionality of the math used.
Under the specific condition that $|Z_1| = |Z_N|$, we can achieve the desired outcomes of both examples listed above: $f(\mu)=\frac{\alpha + \omega}{2}$, $f(x_1)=\alpha$, and $f(x_N) = \omega$, using either method of calculation for $\sigma'$ and $\mu'$. When we normalize scores, it will always be true that $|Z_1| = |Z_N|$, so we will default to this method of curving should we choose a range curve.

Example: Setting our new intended range as $\alpha = 60$ and $\omega = 100$, and curving the dataset $X=\{20 , \ $$ 44 , \ $$ 48 , \ $$ 52 , \ $$ 76\}, \ \mu=48 $, we arrive at roughly $\{60 , \ $$ 77.14 , \ $$ 80 , \ $$ 82.86 , \ $$ 100\}$. Here the mean, $48$ is curved to the center of the new range, $80$, and the extrema, $20$, and $76$ are curved to the edges of the range $60$ and $100$.

Distribution, Curves, and Normality

Probability distribution functions give the chance of different outcomes happening. The term curve, or bell curve, comes from the shape of a normal distribution. A normal distribution, seen below, refers to a distribution where numerical outcomes near the average are more common than outcomes further from the average. These types of distributions are extremely common in statistics and arise in test grades, and IQ tests, as well as height, top speed, and many other natural characteristics.

Normal distributions, have a more rigorous and motivated definition. For further discussion see video here (content not owned by Curve Genius).
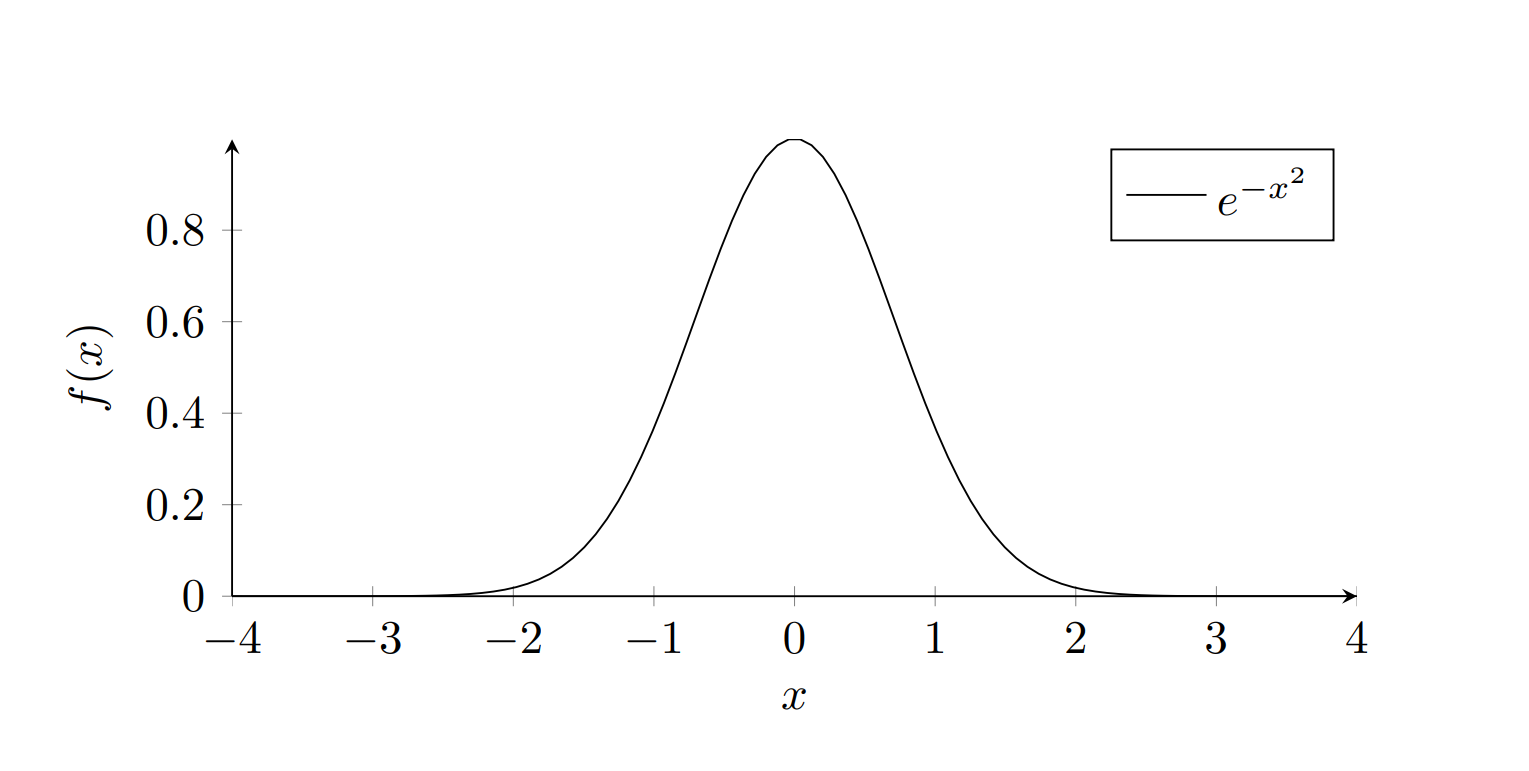
Image of Normal Distribution

*Disclaimer:* the commonly excepted equation for a normal distribution is a scaled version of the equation above: $\frac{1}{\sqrt{2 \pi}} e^{\frac{-x^2}{2}}$.

If a distribution of scores does not seem normal (i.e, scores do not seem to be more common near the average), one might want to normalize it so that grades like Bs and Cs are more common than As and Ds. During the normalization process, large gaps in scores will be closed, and outliers (exceedingly high or low scores will be brought toward the new mean after curving). This has pros and cons.

Example: If on a given test, all students score between $45\%$ and $60 \% \ $ except one student who scores $85\%$, this student's new score will still be the highest, but will not be much greater than the new score of the second highest scorer (who, in this scenario, originally scored near $60\%$).

To normalize a distribution, we generate a probability basket for each element and use it to generate a Z-score. With our dataset $X$, we want to divide the probability distribution into $N$ baskets such that if $N=10$, the 1st will be between the 0th and 10th percentile of the distribution, the 2nd between the 10th and 20th percentile, and so on. To equally space each element within the new distribution, we will make it so that each element's percentile is centered in its probability basket. This generates the equation $$P(x < Z'_i) = \frac{2i-1}{2N}$$ where $x$ is a random score in the distribution and $Z'_i$ represents the new Z-score of the nth element in $X$.

From the definitions of a probability distribution function and a normal distribution it follows that $$P(x < q) = \frac{1}{\sqrt{2 \pi}}\int_{- \infty }^q e^{\frac{-t^2}{2}} dt$$ where $x$ and $q$ are scores in the distribution. Putting this together we get $$ \frac{2i-1}{2N} = \frac{1}{\sqrt{2 \pi}}\int_{- \infty }^{Z'_i} e^{\frac{-x^2}{2}} dx$$ Solving for the new Z-score we get $$ Z'_i = \sqrt{2} {\textrm{erf}^{-1}} \left( \frac{2i-1}{N}-1 \right) $$ If multiple elements are equal, it follows that they should have the same new Z-score. In this case, we replace the value $i$ in the formula above with the average index of elements that share the same value. Because the dataset is ordered, the indices are consecutive, and the average equals $i + \frac{k-1}{2}$ where $k$ is the number of times the element's score appears and $i$ is the index of the first element with the given score. For example, the new Z-score of an element $x_i$ that repeats $k$ times and has the lowest possible index of $i$ is $$ Z'_i = \sqrt{2} {\textrm{erf}^{-1}} \left( \frac{2i + k-2}{N}-1 \right) $$ Note, that if an element only appears once (i.e. $k=1$), then the formula remains the same as derived above.

Example: Using the method above to generate a normalized dataset of 10 scores and rounding to decimals, we get $\{ -1.64 , \ $ $ -1.04 , \ $ $ -0.67 , \ $ $ -0.39 , \ $ $ -0.13, \ $ $ 0.13, \ $ $ 0.39, \ $ $ 0.67, \ $ $ 1.04, \ $ $ 1.64 \}$. The P-value for this dataset is $1$, indicating it is exactly expected from a normal distribution.

After creating the normalized Z-scores for our dataset, we can use them in our curve function in place of the previous Z-scores.

Curving this with a mean and deviation curve and using $\mu = 80, \ \sigma = 8 $ our result is $ \{ 66.84, \ $ $ 71.71 , \ $ $ 74.6, \ $ $ 76.92, \ 78.99, \ $ $ 81.01, \ $ $ 83.08, \ $ $ 85.4, \ $ $ 88.29, \ $ $ 93.16 \}$. Curving this with a range curve and using $ \alpha=60, \ \omega = 100 $ we get $\{60, \ $ $ 67.39, \ $ $ 71.8, \ $ $ 75.31, \ $ $ 78.47, \ $ $ 81.53, \ $ $ 84.69, \ $ $ 88.2, \ $ $ 92.61, \ $ $ 100 \} $.